Jarang sekali dapat
beruntung mengetahui ragam populasi induk (asal) tempat kita menarik contoh.
Untuk contoh berukuran n≥ 30, nilai dugaan yang baik bagi σ2
diberikan oleh s2. Dengan
demikian apa yang terjadi dengan sebaran nilai-nilai z dalam Dalil Limit Pusat bila kita mengganti σ2 dengan s2. Asalkan s2 merupakan nilai dugaan
yang baik bagi σ2 dan tidak terlalu bervariasi dari contoh satu ke
contoh lainnya, dan inilah yang terjadi bila n≥ 30, maka nilai-nilai
masih menyebar menghampiri
sebaran normal baku, sehingga Dalil Limit Pusat tetap berlaku.
Bila ukuran contohnya kecil (n< 30), nilai-nilai s2 berfluktuasi cukup besar
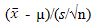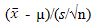dari contoh satu ke cotoh lainnya, dan sebaran nilai-nilai tidak lagi normal baku.
Bila demikian halnya, kita sesungguhnya berhadapan dengan sebaran untuk
statistik yang disebut T, yang
nilai-nilainya adalah
tidak lagi normal baku.
Bila demikian halnya, kita sesungguhnya berhadapan dengan sebaran untuk
statistik yang disebut T, yang
nilai-nilainya adalah
yang merupakan sebuah nilai peubah acak T yang mempunyai
sebaran t dengan v = n – 1 derajat
bebas.
Pada tahun 1908, W.S. Gosset mempublikasikan sebuah
makalah yang memuat keberhasilannya menurunkan sebaran peluang bagi T. Pada
waktu itu, Gosset bekerja pada sebuah pabrik bir milik orang Irlandia yang
tidak mengizinkan publikasi hasil-hasil penelitian para stafnya. Untuk
mengatasi hal ini, ia mempublikasikan karyanya itu dibawah nama samaran ”Student”. Sejak itu, sebaran bagi T
disebut sebaran t-Student atau
ringkasnya sebaran t.
Sebaran t menyerupai sebaran z, dalam hal keduanya
setangkup di sekitar nilai tengah nol. Kedua sebaran tersebut berbentuk genta
namun, sebaran t lebih bervariasi, berdasarkan kenyataan bahwa nilai t
bergantung pada fluktuasi dua besaran yaitu x dan s2, sedangkan
nilai z bergantung pada perubahan x dari satu contoh ke contoh lainnya. Sebaran
bagi t berbeda dengan sebaran bagi z dalam hal ragamnya bergantung pada ukuran
contoh n dan selalu lebih besar dari 1. Hanya bila ukuran contoh 
kedua sebaran itu
menjadi sama.
kedua sebaran itu
menjadi sama.
Gambar 1.
Sifat Kesetangkupan Sebaran t
Adapun ciri – ciri dari
distribusi adalah sebagai berikut:
1.
Distribusi ini digunakan jika ukuran sampel yang
digunakan sangat kecil, yaitu n < 30.
2.
Distribusi ini bergantung pada nilai mean dan simpangan baku masing-masing
sampel yang berfluktuasi sangat besar.
3. Distribusi ini akan
sama dengan distribusi normal apabila jumlah sampel sangat besar.
Tidak ada komentar:
Posting Komentar